条件概率问题

1. 一个家庭有两个孩子，求当其中有一个是男孩时，另一个是男孩的概率（答案1/3）
2. 一个家庭有两个孩子，求当其中有一个是出生在星期二的男孩时，另一个是男孩的概率(答案13/27)

这个两个问题本身并不不复杂，但是我想到了一些奇怪的东西。
我们知道，解概率问题的一般流程是：

!. 找到每个事件的不可拆分的最小单元，由这些事件组成的集合叫做基本事件空间，列出基本事件空间

例如投掷一枚骰子，基本事件空间为

Ω = {1点向上,2点向2...6点向上}

好像很河狸……那现在有一个问题，1点向左这个事件算在这个基本事件空间之内吗？
显然是不算的

所以投掷一枚骰子，完整的事件空间应该是

Ω = {1点向上，1点向下，1点向左，1点向右，2点向上，2点向上，2点向左，2向右 <以此类推...> 6点向右}

即

【思考】对吗？ 好像又不太对，显然，我们平常研究投骰子的问题，好像不会用这种概率空间……
于是问题出在哪里呢？

所以我们会发现，基本事件空间如何确定取决于研究的具体问题，并不是把一切可能的情况全部列出来，而对于具体的研究问题，事件上，我们根据具体的问题的限定词来修正基本事件空间

【问题1 】投掷一枚骰子，投出3点的概率？
这里的基本事件空间是

Ω = {投出1点,投出2点,投出3点,投出4点,投出5点,投出6点}

【问题2】 投掷一枚骰子，3点向上的概率？（由于这里多了一个限定词“向上”，于是我们的概率空间会被扩大）

Ω = {1点向上，1点向下，1点向左，1点向右，2点向上，2点向上，2点向左，2向右 <以此类推...> 6点向右}

然后你一定会奇怪，凭经验，这个问题的答案应该依然是1/6，这是为什么呢？
【经验修正】
因为我们的经验默认了一个大前提，只看向上这种情况的点数，这点被这个问题隐藏了，即1/6这个答案，我们对问题实际上是这样限定的：

投掷一枚骰子，当点数向上的时候，3点向上的概率？

我们把带有条件的概率称作条件概率，概率函数用P()表示，那么这个问题用条件概率可以表示为：
p(3点向上|点数向上)
根据条件概率公式：
P(A|B) = P(AB) / P(B)
即 当B事件发生的前提下，A事件发生的概率，等于AB事件同时发生的概率除以B事件发生的概率

$$
P(3点向上 \mid 点数向上)
= \frac{P(3点向上 \cdot 点数向上)}{P(点数向上)}
$$

p(3点向上且点数向上) = 1/24
p(点数向上) = 6 / 24

于是 二者一除，消去了分母24，是我们想要的结果1/6。

但是，问题还没有结束，我们回到一开始的问题，解概率问题的基本流程是

!. 找到每个事件的不可拆分的最小单元，由这些事件组成的集合叫做基本事件空间，列出基本事件空间
2. 将概率问题的中文翻译成集合运算

这里我们认为 + 符号 等价于 ∪符号， * 符号 等价于 ∩符号
比如 A发生或B发生 翻译成 A∪B = A+B
A发生且B发生 翻译成 A∩B = A*B = AB
由于集合可以有运算律，我们可以混合运算

A(B+C) = AB + AC

利用代数公式变形，我们可以把难以理解的复杂问题转化为简单问题

3. 将集合运算带入概率函数P()，使用概率公式
   例如 P(A(B+C)) = P(AB+AC)
   此时可以带入概率加法公式，即
   p(AB+AC) = P(AB) + P(AC) -P(AB * AC)

4. 化简，得出档答案

这个过程有什么问题呢，你会发现，我们不存在带有条件概率符号的集合运算
即如果我们把条件概率和普通集合混合运算例如 (A+B) * A|B = ?
这个结果是什么？
我们发现集合运算上，这一块是空白的

于是当我们有一个符号P(A|B)
有一个可以被算出来的答案X
却发现中间的集合运算A|B是空白的

那这些集合运算去哪儿了？ 集合运算有 A并B 有A交B ，但是 没有 A|B 这个集合运算

这是本文的最后问题
是否能够定义出集合运算A|B表示为一个新集合？
同时给这个运算提供运算律

思考： 我们知道集合运算有笛卡尔积 A X B = ....

今天群里讨论了一道题，来分享下

一天亮亮提前放学，他独自往家走了15分钟，遇到来接 他的爸爸，于是坐上车回家，比平时爸爸准时放学来接 提早了12分钟到家。请问亮亮这天提前多少分钟放学的？

初中数学思维导图

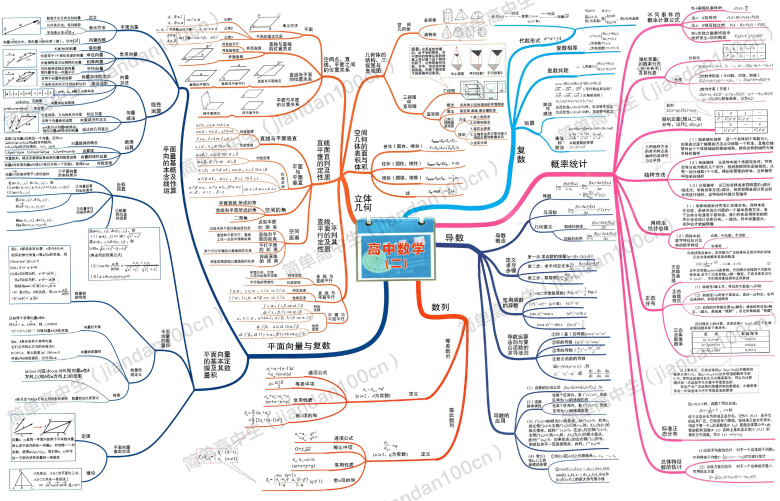
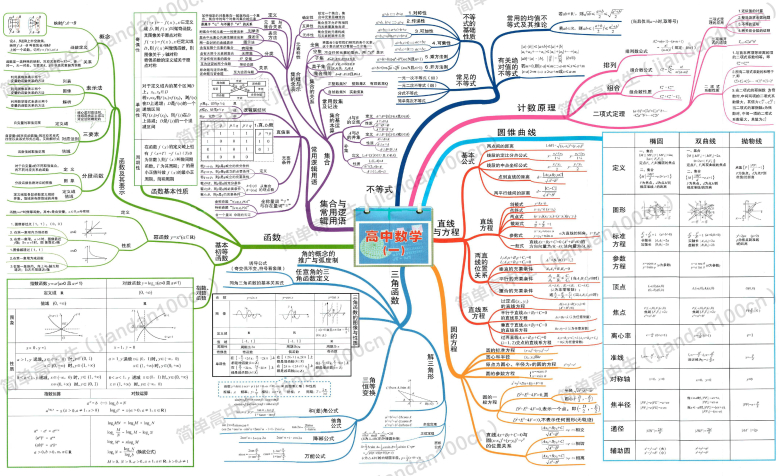
高中数学思维导图

随手找的，好像还挺全的